Inertialization

在Unreal Engine（UE）中，Inertialization（惯性化）是一种动画过渡技术，用于在不同动画状态之间实现平滑的过渡，避免突兀的切换。它通过模拟物理惯性效果，使角色的动作过渡更加自然流畅。

什么是Inertialization？

Inertialization 是 UE 动画系统中的一种过渡机制，主要用于在两个动画状态之间进行插值。传统的动画过渡通常使用线性插值（Lerp）或混合（Blend），但这些方法可能会导致动作不连贯或僵硬。Inertialization 通过模拟物理惯性，使得过渡更加平滑，尤其是在快速切换动画状态时。

为什么需要Inertialization？

在角色动画中，动画状态之间的切换非常频繁。例如，角色从跑步切换到站立，或者从跳跃切换到落地。如果直接切换动画，可能会导致角色的姿势或速度突变，看起来不自然。Inertialization 通过保留前一动画的惯性（如速度、旋转等），使过渡更加平滑。

Inertialization 的工作原理

Inertialization 的核心思想是：在动画切换时，保留前一动画的某些物理属性（如速度、角速度等），并将其应用到新动画的初始状态中。具体步骤如下：

• 检测动画切换：当动画状态发生变化时，系统会检测前一动画的状态。
• 计算惯性：根据前一动画的速度、旋转等属性，计算出惯性值。
• 应用惯性：将惯性值应用到新动画的初始状态，使过渡更加平滑。
• 衰减惯性：随着时间的推移，惯性效果逐渐衰减，直到完全过渡到新动画。

以上讲的是从整个动画的角度来看，我们从微观的角度来看，把这个问题细化。正常的混合是将两个姿势的每个骨骼进行插值，每个骨骼有位置，旋转，缩放信息。再次细化就是分别对向量和四元数做插值，常用的方式向量就是线性插值，四元数就是球面插值。再细化向量的线性插值，就是对两个浮点数做线性插值，也就是下面公式：

x = a + (b-a) * t

惯性化插值计算整个流程跟正常插值差不多，只是计算两个浮点数插值的公式与上面的计算公式不同。下面简单讲解一下惯性化插值如何计算：

CalcInertialFloat

其核心算法在AnimNode_Inertialization.cpp中的：

static float CalcInertialFloat(float x0, float v0, float t, float t1)

CalcInertialFloat 函数通过一个五次多项式曲线（quintic polynomial curve）来模拟一个物理系统中的惯性运动，实现了从初始值到零值的平滑过渡，确保在结束时速度和加速度也为零。这种技术在需要平滑过渡的场景中非常有用，尤其是在动画和物理模拟中。

函数参数

• x0: 初始值（时间 t=0 时的值）。
• v0: 初始速度（时间 t=0 时的一阶导数）。
• t: 当前时间，用于计算惯性化值。
• t1: 惯性化结束时间，即曲线在该时间点必须为零。

函数逻辑

1. 时间边界检查:

   • 如果 t 小于 0，将其设置为 0。
   • 如果 t 接近或超过 t1，直接返回 0，因为此时曲线已经结束。

2. 符号处理:

   • 如果 x0 为负值，将其取反，并相应地调整 v0 和最终结果的符号。

3. 速度限制:

   • 如果 v0 为正，将其设置为 0，以防止曲线在过渡过程中出现“过冲”（overshoot）。

4. 输入有效性检查:

   • 确保 x0、v0、t 和 t1 都是有效的非负值。如果无效，将所有值重置为 0。

5. 调整结束时间 t1:

   • 如果 v0 为负且较大，调整 t1 以确保曲线不会在过渡过程中出现负值（即确保 x >= 0 对于所有 t 在 0 到 t1 之间）。

6. 计算初始加速度 a0:

   • 计算一个初始加速度 a0，使得曲线在 t1 时速度、加速度和加加速度（jerk，三阶导数）都为零。如果计算出的 a0 为负，则将其设置为 0。

7. 计算多项式系数:

   • 根据初始条件和结束条件，计算五次多项式的系数 A、B、C 和 D。

8. 计算当前值 x:

   • 使用计算出的多项式系数和当前时间 t，计算当前的值 x。

9. 返回结果:

   • 根据之前的符号处理，返回最终的惯性化值。

关键点

• 五次多项式：使用五次多项式可以确保曲线在结束时不仅值为零，而且速度和加速度也为零，从而实现平滑的过渡。
• 防止过冲：通过调整 t1 和限制 v0，确保曲线在过渡过程中不会出现负值。
• 初始加速度 a0：通过计算一个合适的初始加速度，确保曲线在结束时满足所有条件。

Vector

将向量转化为：

• 方向
• 长度，对长度惯性化插值

Quaternion

将四元数转化为：

• 旋转轴
• 旋转角，对角度惯性化插值

Inertialization 的优点

• 平滑过渡：避免了动画切换时的突兀感，使动作更加自然。
• 减少人工调整：传统动画过渡需要手动调整混合时间或曲线，而 Inertialization 可以自动处理。
• 适用于复杂动画：特别适合快速切换的复杂动画状态，如战斗、运动等。

如何在 UE 中使用 Inertialization？

在 UE 中，Inertialization 默认集成在动画蓝图中。你可以通过以下方式启用或调整它：

• 动画蓝图：在动画蓝图中，Inertialization 通常会自动应用于状态机中的过渡。你可以通过调整过渡设置来控制惯性效果。
• 细节面板：在动画蓝图的过渡节点中，可以找到与 Inertialization 相关的参数，如惯性时间、衰减速度等。

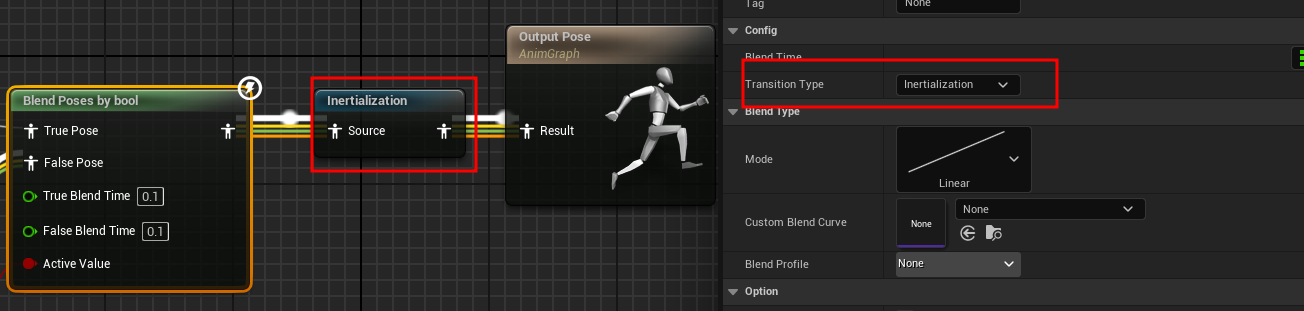
示例场景

假设角色从跑步切换到站立：

• 传统方法：直接切换到站立动画，可能会导致角色突然停止，看起来不自然。
• Inertialization：系统会保留跑步时的速度惯性，使角色逐渐减速并过渡到站立状态，看起来更加真实。

注意事项

• 性能开销：Inertialization 需要计算惯性值，可能会增加一定的性能开销。
• 参数调整：需要根据具体动画调整惯性时间和衰减速度，以达到最佳效果。
• 不适合所有场景：某些动画切换（如瞬间的姿势变化）可能不需要惯性化。

Blending VS Inertialization

混合（Blending）	惯性化（Inertialization）
在过渡期间同时计算源（Source）和目标（Target）状态	在过渡期间仅评估目标（Target）状态
动画帧成本可变	动画帧成本固定
在过渡期间管理多组状态	在过渡期间仅维护一组状态
增加复杂度	简单易用，无需持续管理

看上面那张图可以看出两种混合方式的不同。如果当前节点选择惯性化插值，并不会立马计算，只是会把信息注册到惯性化混合节点中，后面一起计算。举个例子：

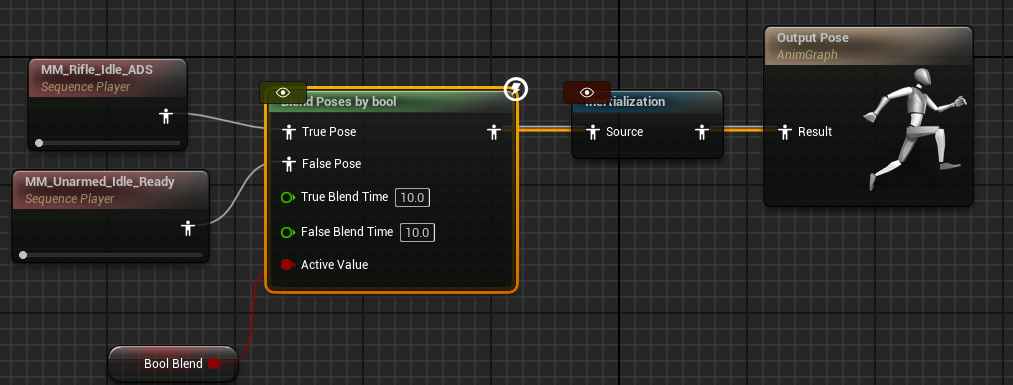
上面Blend Poses by bool节点中选择使用惯性化混合，当Bool Blend值为真时，该节点会直接输出MM_Rifle_Idle_ADS动画，效果如下：

• 黄色骨骼：Blend Poses by bool 节点
• 橙色骨骼：Inertialization 节点

可以看到黄色骨骼立马变换为MM_Rifle_Idle_ADS姿势了，换句话说Blend Poses by bool节点不会做任何操作，输出目标姿势即可，交给Inertialization节点来进行混合。

对比看一下，选择标准的混合方式：

可以看到橙色和黄色重合了，Blend Poses by bool节点开始执行标准的混合操作了。

惯性化动画节点

这里讲解一下该节点动画系统中执行逻辑：

RequestInertialization

首先在其他节点中发起惯性化混合请求，示例代码如下：

UE::Anim::IInertializationRequester* InertializationRequester = ContextGetMessage<UE::Anim::IInertializationRequester>();
if (InertializationRequester)
{
	FInertializationRequest Request;
	Request.Duration = CurrentBlendTimes[ChildIndex];
	Request.BlendProfile = CurrentBlendProfile;
	Request.bUseBlendMode = true;
	Request.BlendMode = GetBlendType();
	Request.CustomBlendCurve = GetCustomBlendCurve();
#if ANIM_TRACE_ENABLED
	Request.NodeId = Context.GetCurrentNodeId();
	Request.AnimInstance = Context.AnimInstanceProxy->GetAnimInstanceObject();
#endif

	InertializationRequester->RequestInertialization(Request);
	InertializationRequester->AddDebugRecord(*Context.AnimInstanceProxy, Context.GetCurrentNodeId());
	bRequestedInertializationOnActiveChildIndexChange = true;
}

请求会放在队列中：

RequestQueue.AddUnique(FInertializationRequest(Duration, BlendProfile));

在FAnimNode_Inertialization::Evaluate_AnyThread中对其处理。

Set Inertialization Duration

设置惯性化混合时间，选择请求队列中最大的混合时间。并通过混合描述文件对每根骨骼设置混合时间。

// Cache the maximum duration across all bones (so we know when to deactivatethe inertialization request)
InertializationMaxDuration = FMath::Max(InertializationDuration, *Algo::MaxElement(InertializationDurationPerBone));

Detect Teleport

比较这一帧和上一帧的根节点的世界坐标，大于GetSkelMeshComponent()->GetTeleportDistanceThreshold()的值，就停止混合。

Update The Inertialization Timer

更新当前混合时间InertializationElapsedTime，并处理结束混合:

if (InertializationState != EInertializationState::Inactive)
{
	InertializationElapsedTime += DeltaTime;
	if (InertializationElapsedTime >= InertializationDuration)
	{
		// Reset the deficit accumulator
		InertializationDeficit = 0.0f;
	}
	else
	{
		// Pay down the accumulated deficit caused by interruptions
		InertializationDeficit -= FMath::Min(InertializationDeficit, DeltaTime);
	}

	if (InertializationElapsedTime >= InertializationMaxDuration)
	{
		Deactivate();
	}
}

Inertialize The Pose

计算目标姿势与前一个姿势之间的惯性化姿势差，并计算该差值的速度：

void FAnimNode_Inertialization::InitFrom(const FCompactPose& InPose, const FBlendedCurve& InCurves, const FTransform& ComponentTransform, const FName AttachParentName, const FInertializationSparsePose& Prev1, const FInertializationSparsePose& Prev2)

其中InPose是目标姿势。分别计算出没根骨骼对应的以下这些数据：

• TArray<int32> BoneIndices;
• TArray<FVector3f> BoneTranslationDiffDirection;
• TArray<float> BoneTranslationDiffMagnitude;
• TArray<float> BoneTranslationDiffSpeed;
• TArray<FVector3f> BoneRotationDiffAxis;
• TArray<float> BoneRotationDiffAngle;
• TArray<float> BoneRotationDiffSpeed;
• TArray<FVector3f> BoneScaleDiffAxis;
• TArray<float> BoneScaleDiffMagnitude;
• TArray<float> BoneScaleDiffSpeed;

Apply The Inertialization Offset

将惯性化差值应用于给定的姿势（当 ElapsedTime 接近 Duration 时衰减为零），对每根骨骼单独计算：

const float Duration = InertializationDurationPerBone[SkeletonPoseBoneIndex];
// Apply the bone translation difference
const FVector T = (FVector)BoneTranslationDiffDirectio[InertializationBoneIndex] *
	UE::Anim::Inertialization::Private::CalcInertialFloat(BoneTranslationDiffMagnitude[InertializationBoneIndex], BoneTranslationDiffSpeed[InertializationBoneIndex], InertializationElapsedTime, Duration);
InOutPose[BoneIndex].AddToTranslation(T);

// Apply the bone rotation difference
const FQuat Q = FQuat((FVector)BoneRotationDiffAxis[InertializationBoneIndex],
	UE::Anim::Inertialization::Private::CalcInertialFloat(BoneRotationDiffAngle[InertializationBoneIndex], BoneRotationDiffSpeed[InertializationBoneIndex], InertializationElapsedTime, Duration));
InOutPose[BoneIndex].SetRotation(Q * InOutPose[BoneIndex].GetRotation());

// Apply the bone scale difference
const FVector S = (FVector)BoneScaleDiffAxis[InertializationBoneIndex] *
	UE::Anim::Inertialization::Private::CalcInertialFloat(BoneScaleDiffMagnitude[InertializationBoneIndex], BoneScaleDiffSpeed[InertializationBoneIndex], InertializationElapsedTime, Duration);
InOutPose[BoneIndex].SetScale3D(S + InOutPose[BoneIndex].GetScale3D());

Record Pose Snapshot

缓存姿势：

if (!CurrPoseSnapshot.IsEmpty())
{
	// Directly swap the memory of the current pose with the prev pose snapshot (to avoid allocations and copies)
	Swap(PrevPoseSnapshot, CurrPoseSnapshot);
}

// Initialize the current pose
CurrPoseSnapshot.InitFrom(Output.Pose, Output.Curve, ComponentTransform, AttachParentName, DeltaTime);

五次多项式

五次多项式（Quintic Polynomial）是指最高次项为五次的多项式函数，通常表示为：

[
P(t) = At^5 + Bt^4 + Ct^3 + Dt^2 + Et + F
]

其中，(A, B, C, D, E, F) 是多项式的系数，(t) 是自变量（通常是时间）。

---

五次多项式的特点

1. 高阶平滑性：

   • 五次多项式是一个高阶函数，具有连续的一阶、二阶、三阶甚至更高阶导数。
   • 这种平滑性使得它在需要高度控制的场景中非常有用，例如动画、机器人路径规划、物理模拟等。

2. 灵活性：

   • 五次多项式有六个系数（(A, B, C, D, E, F)），因此可以通过六个独立的约束条件来确定这些系数。
   • 例如，可以指定函数在起点和终点的值、速度（一阶导数）、加速度（二阶导数）等。

3. 无振荡性：

   • 相比于低阶多项式（如三次多项式），五次多项式更容易避免振荡（overshoot 或 undershoot），尤其是在需要满足多个边界条件时。

---

为什么使用五次多项式？

在惯性化（Inertialization）或平滑过渡的场景中，五次多项式被广泛使用，因为它可以满足以下条件：

1. 位置约束：指定起点和终点的值（例如，从 (x_0) 过渡到 0）。
2. 速度约束：指定起点和终点的速度（例如，起点速度为 (v_0)，终点速度为 0）。
3. 加速度约束：指定起点和终点的加速度（例如，起点加速度为 (a_0)，终点加速度为 0）。
4. 加加速度约束：如果需要，还可以指定起点和终点的加加速度（jerk，三阶导数）。

通过五次多项式，可以同时满足这些约束条件，从而实现平滑且可控的过渡。

---

五次多项式的应用

1. 动画和游戏开发：

   • 在角色动画或摄像机移动中，使用五次多项式可以实现平滑的起始和停止，避免突然的跳动或不连续性。

2. 机器人路径规划：

   • 在机器人控制中，五次多项式可以用于生成平滑的运动轨迹，确保机器人的位置、速度和加速度都满足要求。

3. 物理模拟：

   • 在物理引擎中，使用五次多项式可以模拟物体的惯性运动，确保运动在结束时平滑停止。

4. 控制系统：

   • 在控制系统中，五次多项式可以用于设计平滑的控制信号，避免系统的剧烈振荡或不稳定。

---

示例：惯性化中的五次多项式

在 CalcInertialFloat 函数中，五次多项式的形式为：

[
x(t) = At^5 + Bt^4 + Ct^3 + Dt^2 + v_0 t + x_0
]

其中：

• (x_0) 是初始位置（(t=0) 时的值）。
• (v_0) 是初始速度（(t=0) 时的一阶导数）。
• (A, B, C, D) 是通过边界条件计算出的系数。

通过以下约束条件确定系数：

1. 终点位置为零：(x(t_1) = 0)。
2. 终点速度为零：(v(t_1) = 0)。
3. 终点加速度为零：(a(t_1) = 0)。
4. 初始加速度为 (a_0)：(a(0) = a_0)。

这些约束条件可以通过解方程组来确定系数 (A, B, C, D)。

---

总结

五次多项式是一个高阶平滑函数，具有高度的灵活性和可控性。它能够同时满足位置、速度、加速度甚至更高阶导数的约束条件，因此在需要平滑过渡和精确控制的场景中非常有用。在 CalcInertialFloat 函数中，五次多项式被用来实现从初始值到零值的平滑过渡，同时确保速度和加速度在结束时也为零。

Reference

• Inertialization: High-Performance Animation Transitions in Gears of War
  
• https://zhuanlan.zhihu.com/p/390476167
• https://www.gamer.ne.jp/news/202009030009/
• https://www.gdcvault.com/play/1025331/Inertialization
• https://www.gdcvault.com/play/1025165/Inertialization