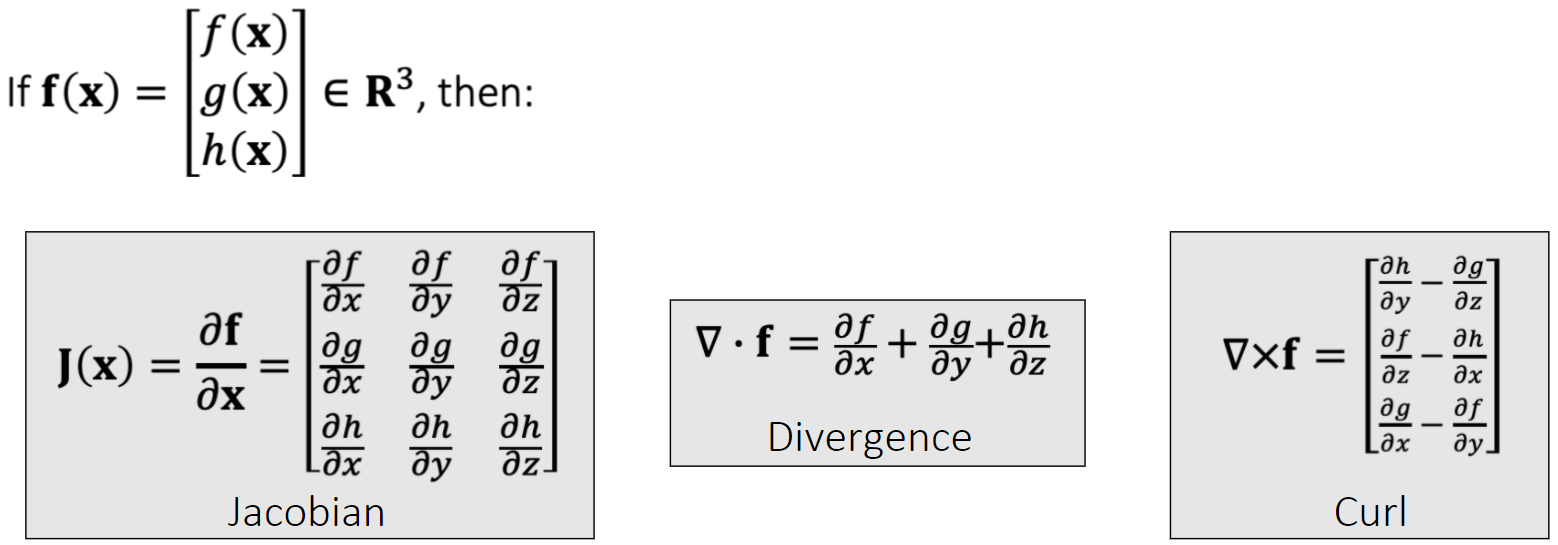Math
December 8, 2021About 2 min
Math
向量
向量实际用的到一些小例子:
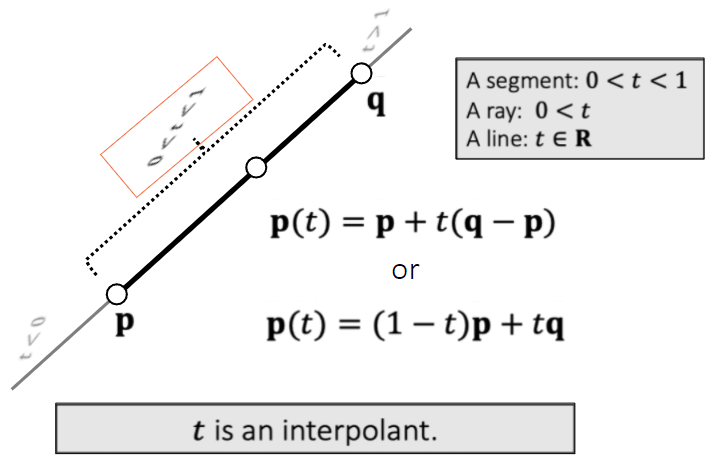
线性插值
两个向量值的插值范围
向量投影
投影计算,已知o,q,v求得 s 点
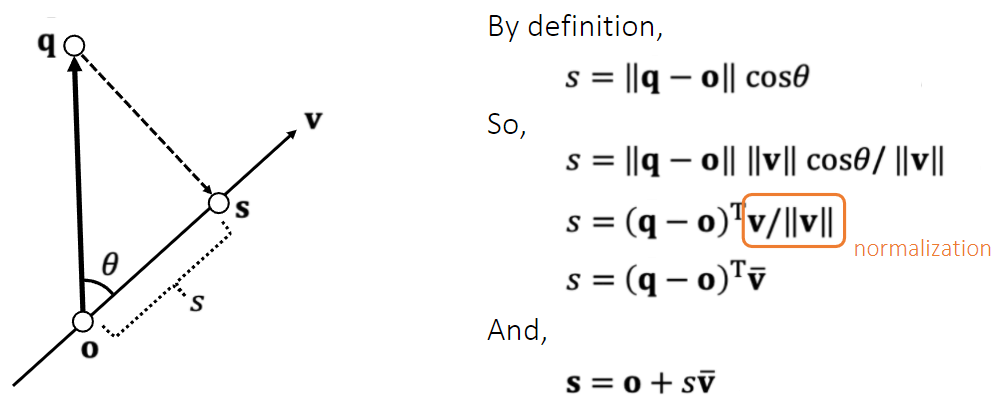
平面判断
判断p点位平面那个方位
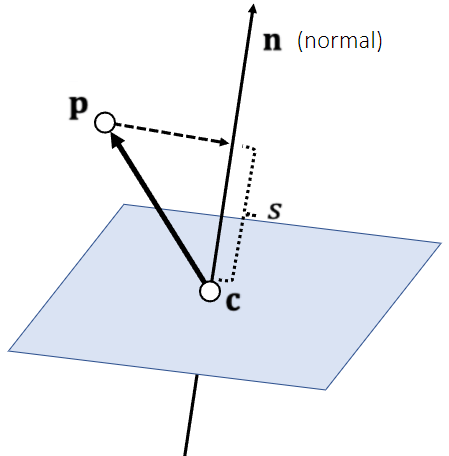
n 为平面的法线,只需要盘点法线和法线与平面交点点乘的结果正负即可。
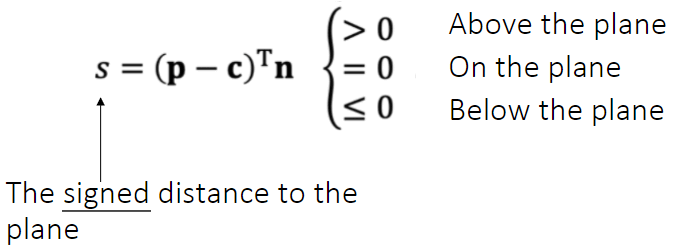
射线与圆的碰撞
我们要求一个从p点出发的射线是否与以c点为圆心半径为r的圆相交也就是发生碰撞
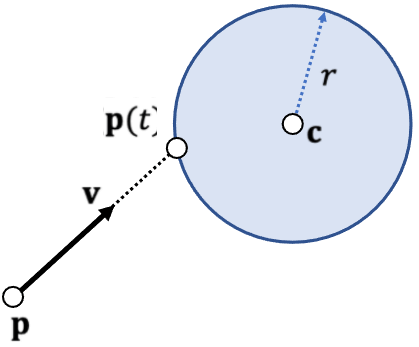
首先我们假设交点为p(t),同时根据插值公式得到:p(t) = p + vt
我们只需要判断p(t)点到c点的距离是否等于圆心即可,就可以得到
||p(t) - c|| = r
两边在平方
||p(t) - c||² = r²
再根据一个向量的模的平方为该向量点乘自己
(p - c + tv) · (p - c + tv) = r²
根据多项式变形得到
(v · v)t² + 2(p - c) · vt + (p - c) · (p - c) - r² = 0
求解二元一次方程即可,一般解有三种情况:
- 没有解:无交点
- 一个解:一个交点
- 两个解:两个交点
三角形的法线与面积
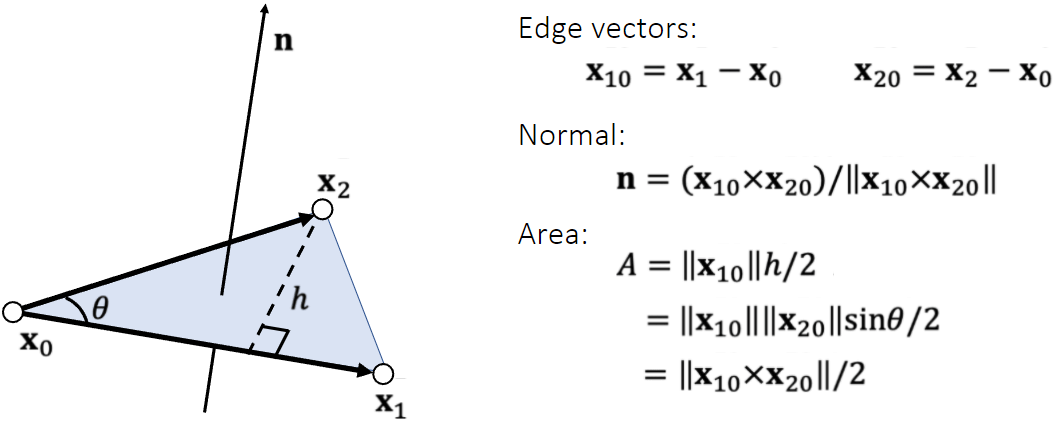
- 叉乘可以获得三角形的法向量和面积
- 法向量方向是根据叉乘的顺序获得
判断一个点是否在三角形内
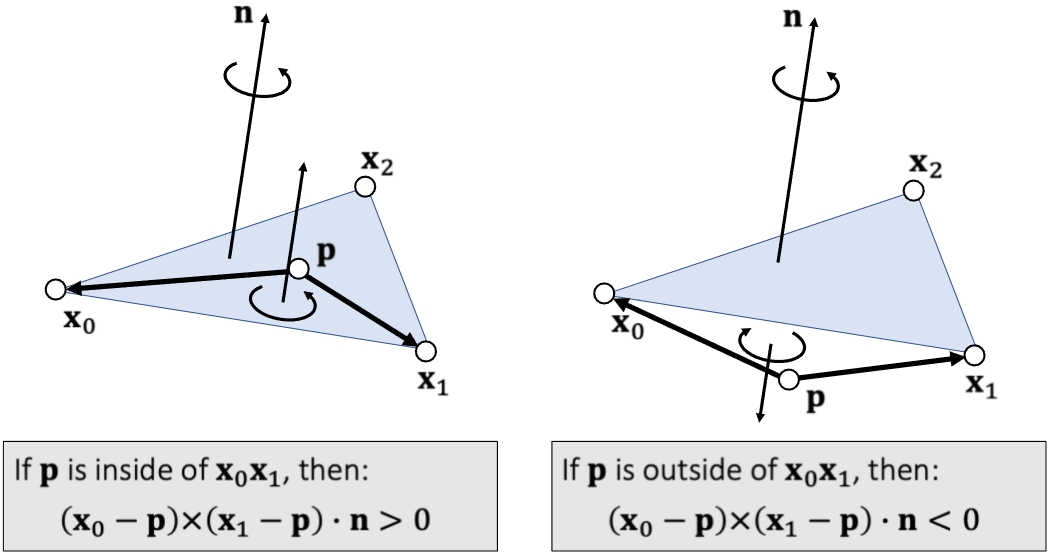
与平面法向量同方向就在 内部
重心
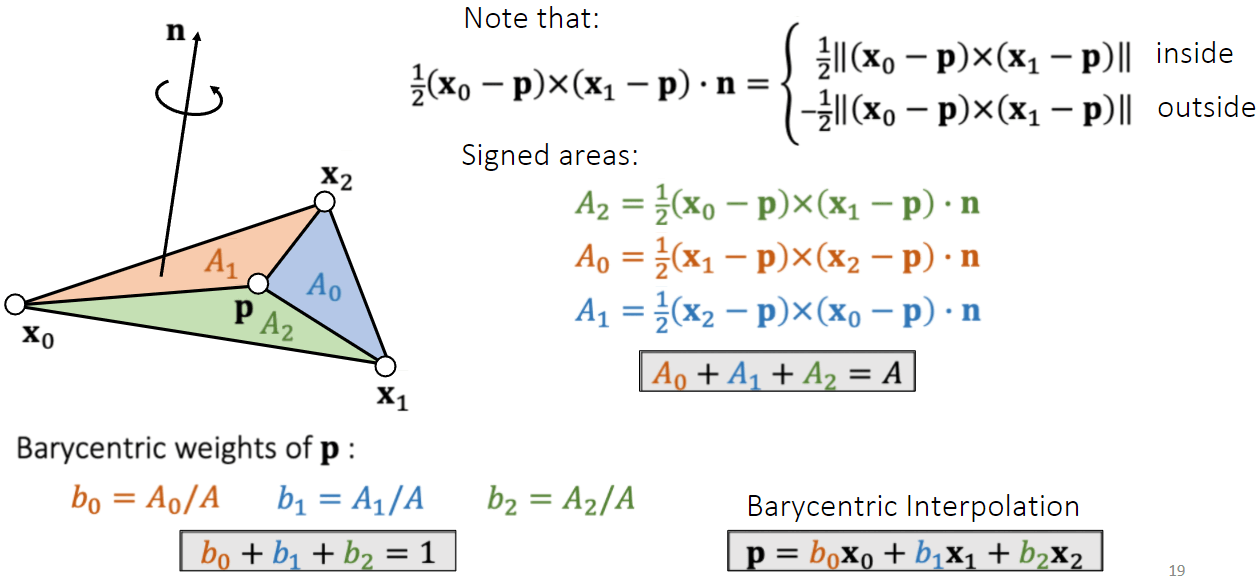
点乘法向量是因为如果点在三角形外面,他的面积就可能是负值。也可以使用线性插值来计算。
使用在三角形着色上。
四面体求体积

四面体重心权重

判断射线是否与三角形相交
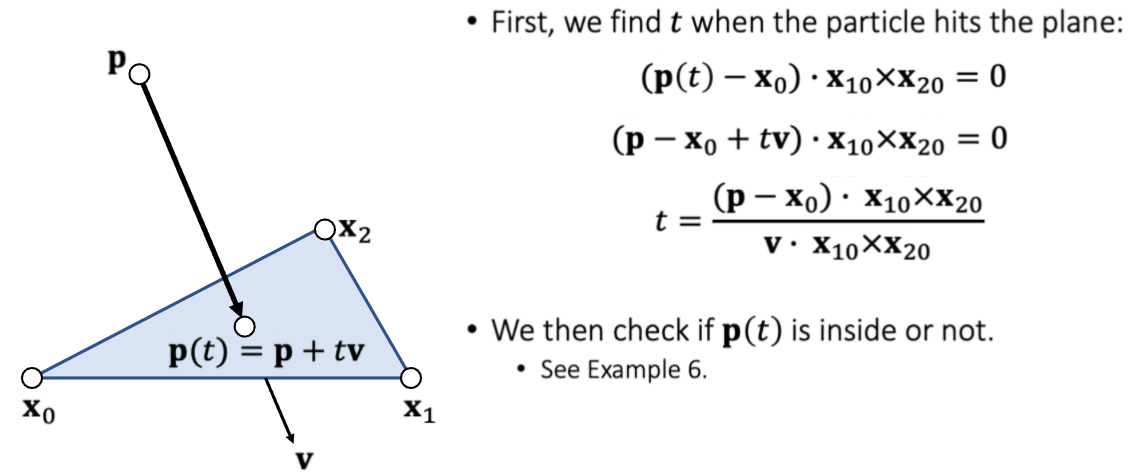
只需要设置一个交点,然后使用交点与任意个顶点相连得到的向量,检测这个向量是否垂直于三角形的法向量 。
矩阵
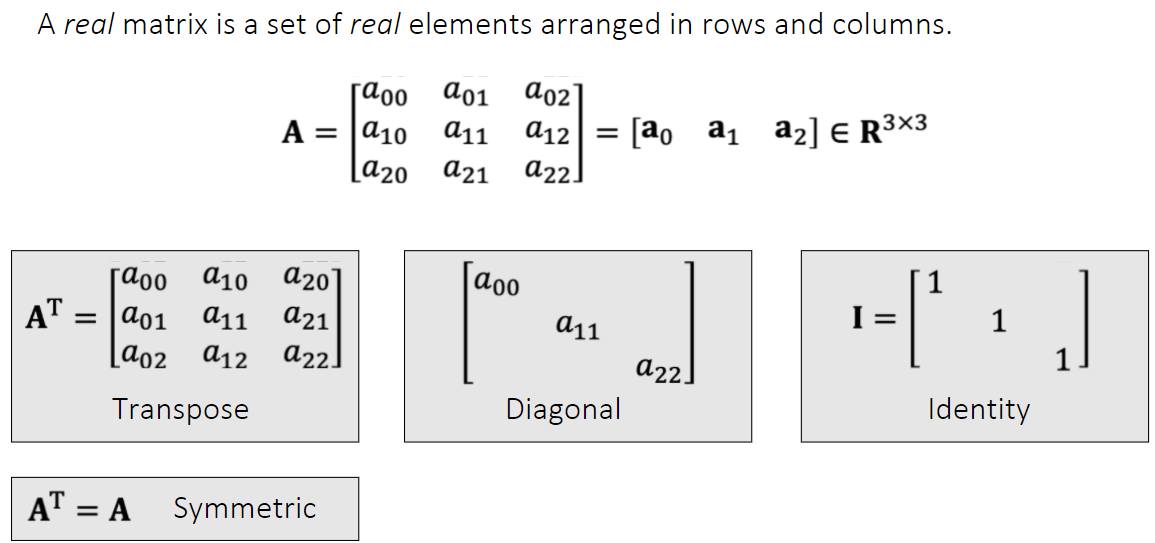
- 转置矩阵
- 对角矩阵,对角线有值,其余地方为0
- 单位矩阵:特殊的对角矩阵
- 对称矩阵
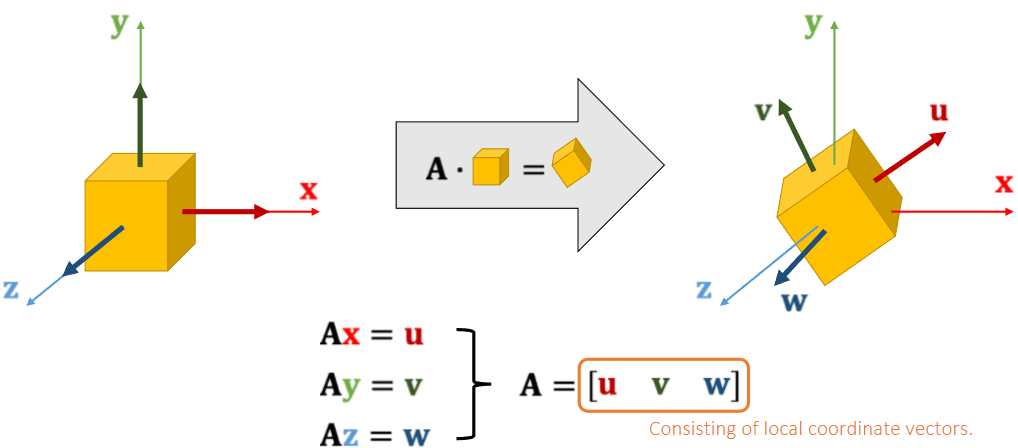
正交矩阵
两两垂直的三个轴

如果使用一个正交矩阵代表着局部坐标,然后对其旋转。
这个旋转矩阵就是描述物体本地坐标的状态。
奇异值分解

任何的线性变化都可以分解成三个步骤:旋转,缩放,旋转
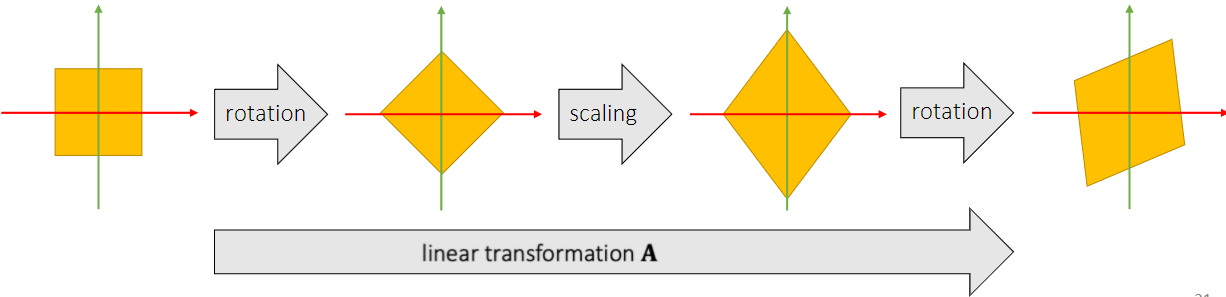
特征值分解
只考虑对称值的特征分解
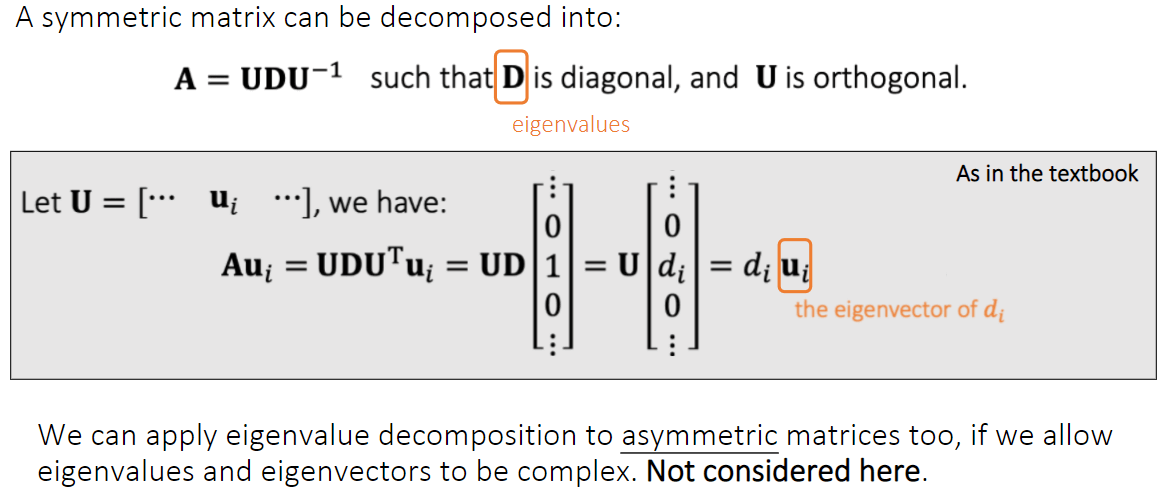
对称
正定矩阵
线性问题
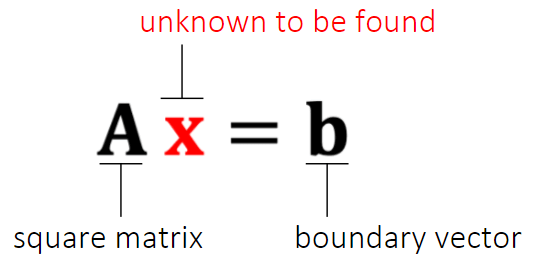
已知矩阵A和结果向量b,需要求解x
一般不使用A的逆来做,因为计算量大和内存消耗大
直接法
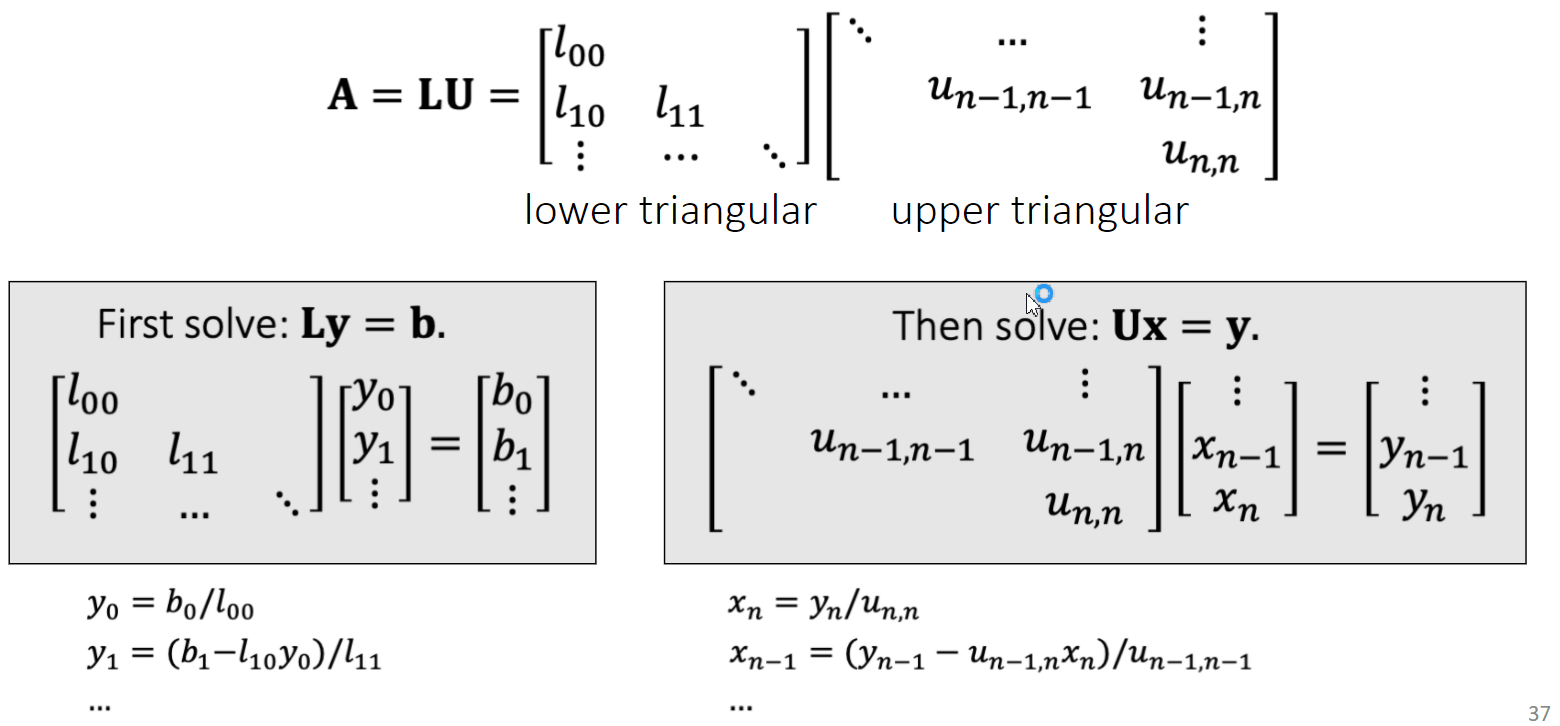
迭代法
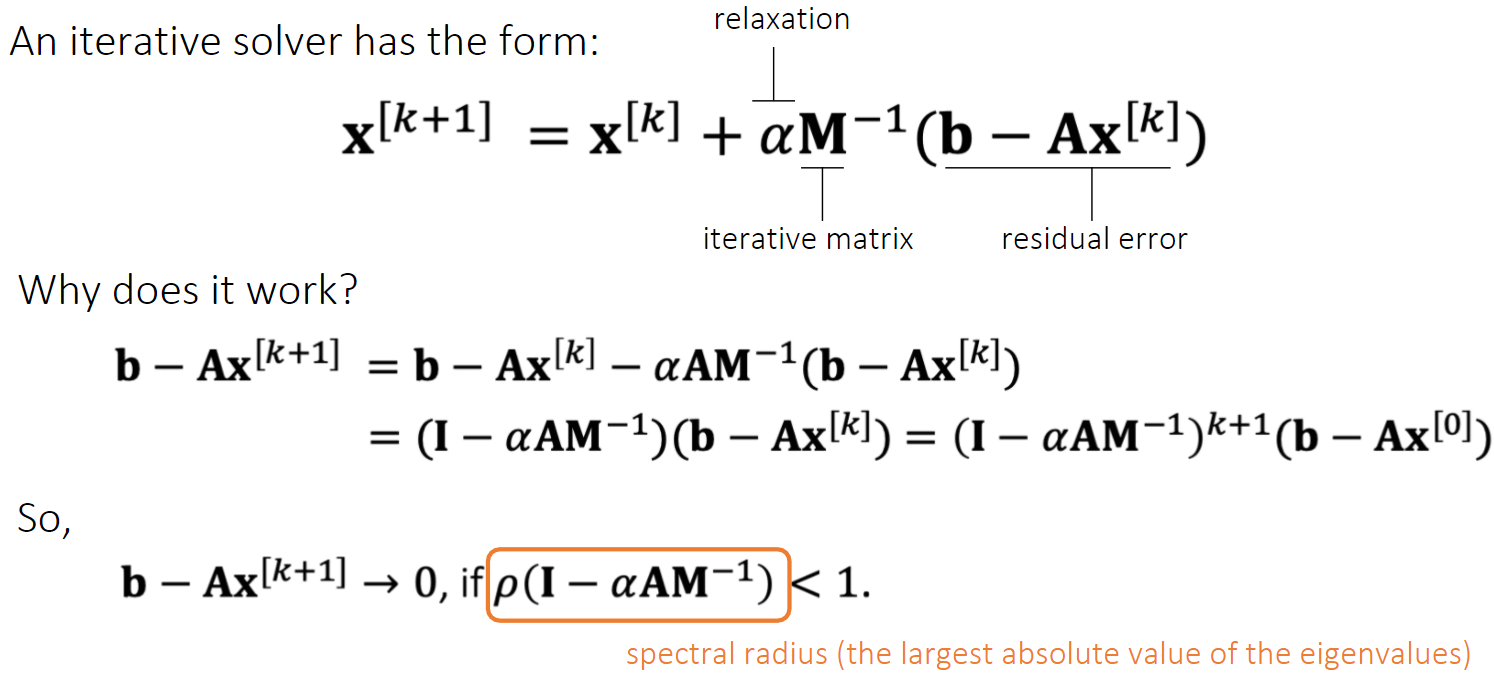
微积分
一阶导数
向量对实数求导
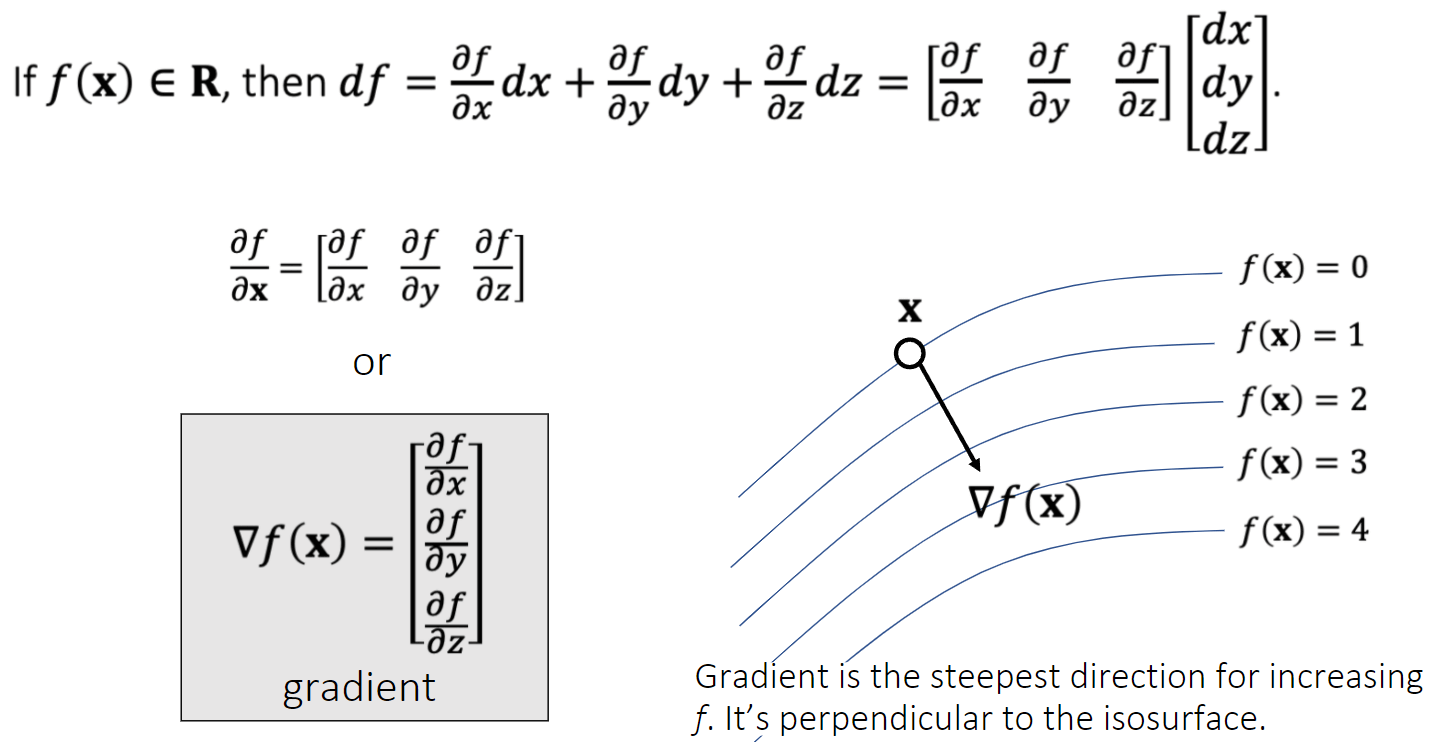
向量对向量求导