Physics-Based Cloth Simulation

January 8, 2022About 2 min

A Mass-Spring System

显示积分有一个问题，如果弹性系数过大，弹簧会来回弹跳。

弹力是一个 holonomic，只跟位置相关的方程。

解决非线性系统

限制：函数需要连续

一阶导数就是在描述一个函数的切方向

对一个函数的一阶导数做一个泰勒展开:

F^{'} (x) \approx F^{'} (x^{(k)}) + F^{″} (x^{(k)}) (x - x^{k})

也就是一阶导数可以是在k位置的一阶导数加上k位置的二阶导数乘以Δx。

方法流程就是：

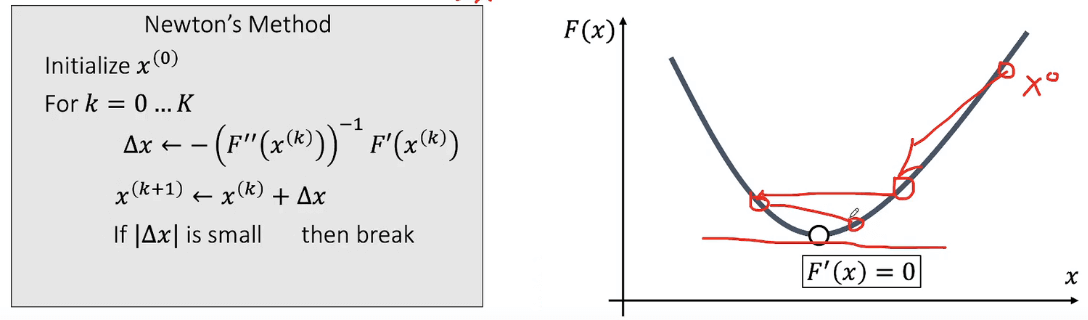
从 $x^{0}$ 开始计算直到Δx足够小时就中断。

函数的一阶导数等于0时，既可以是最大值也可以最小值。可以使用二阶导数来判断是最大值还是最小值：

我们就对每一个顶点模拟，计算它的速度与位置。

我们使用隐式积分计算速度与位置是：

{\begin{cases} v^{[1]} = v^{[0]} + Δ t M^{- 1} f^{[1]} \\ x^{[1]} = x^{[0]} + Δ t v^{[1]} \end{cases}

我们可以用速度计算出位置

{\begin{cases} x^{[1]} = x^{[0]} + Δ t v^{[0]} + Δ t^{2} M^{- 1} f^{[1]} \\ v^{[1]} = (x^{[1]} - x^{[0]}) / Δ t \end{cases}

然后可以转为以下公式，最后对 $x^{[1]}$ 与 $F (x)$ 求导数，得到到梯度 $\nabla (F (x^{[1]}))$ 计算方式。

对于每一个顶点的梯度就是为：

g_{i} = \frac{1}{Δ t^{2}} m_{i} (x_{i} - \tilde{x_{i}}) + f_{i}

这里的力包含了弹力和重力，弹力可以使用公式得到：

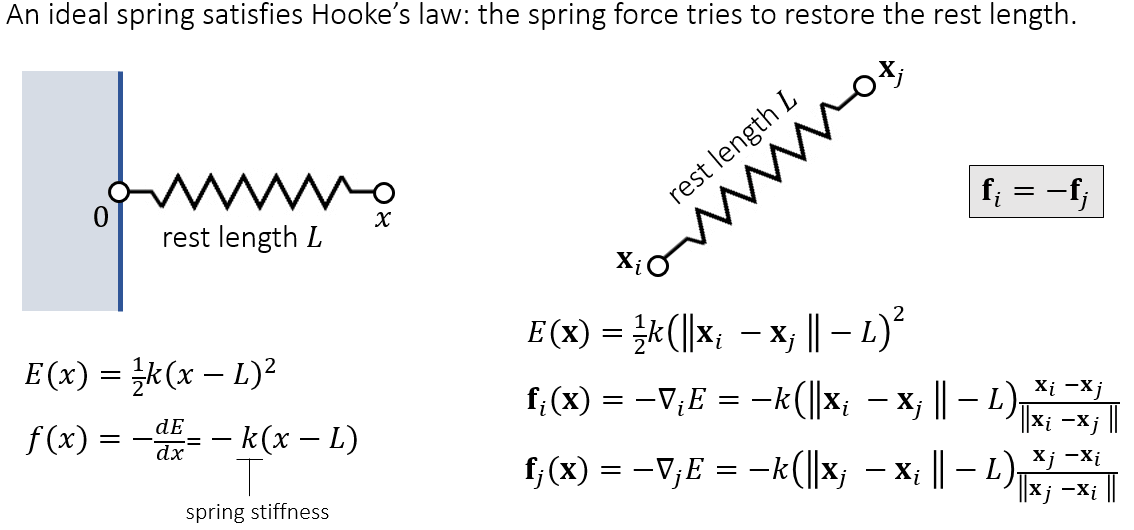
这里每个顶点的弹力是相互的，相加为零。同时一个顶点可能会被多个弹簧相连，所以我们需要计算当前顶点的所有弹力相加。

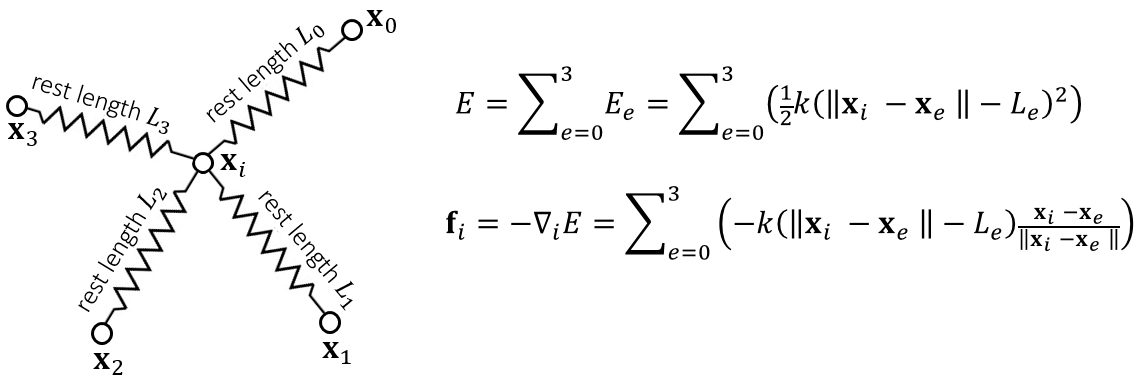
我们就对所有弹簧遍历，对每根弹簧上的顶点计算弹力，然后叠加到梯度上去，我们可以得到公式：

{\begin{cases} g_{i} = g_{i} + k (1 - \frac{L_{e}}{| | X_{i} - X_{j} | |}) (X_{i} - X_{j}) \\ g_{j} = g_{j} - k (1 - \frac{L_{e}}{| | X_{i} - X_{j} | |}) (X_{i} - X_{j}) \end{cases}

我们这里使用简单的方式来代替计算Hessian矩阵，更新位置使用梯度的公式：

X_{i} = X_{i} - (\frac{1}{Δ t^{2}} m_{i} + 4 k)^{- 1} g_{i}

同时再更新速度：

V = V + \frac{1}{Δ t} (X - \tilde{X})

拉伸和弯曲时独立的问题

弹簧锁死翻折

收敛是什么意思？

隐式积分与显示积分的区别？