Skip to main content

Data Structures for Graphics

March 10, 2021About 5 minGraphic

Data Structures for Graphics

  • mesh structures
    用来存储静态网格数据和要来转换

  • spatial data structures

边界分层，空间分层，均匀空间细分

  • scene graph

管理对象和转换

  • tiled multidimensional arraysd

控制性能，

Triangle Meshes

三角形网格处理他们的效率是图形程序最大的工作。

一个网格可以比一个无关联的三角形序列更加效率，因为网格是共用顶点的三角形组成的。

三角形的数据一般包含：

  • 顶点
  • 边界
  • 贴图映射
  • 着色
  • 动画

网格拓扑：三角形链接在一起，不通过顶点的位置信息。

三角形检测条件：

  • 每个边被一个或二个三角形使用
  • 每个顶点了连接到一组边连接的三角形

单个三角形存储需要向前，也就是三个顶点存储的顺序是逆时针

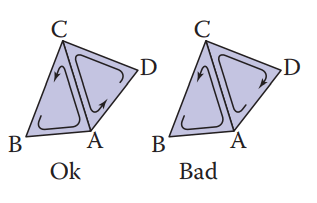
我们在存储三角形顶点位置时，有两种方式：

  • 按三角形存储
  • 按顶点索引存储

如下图：

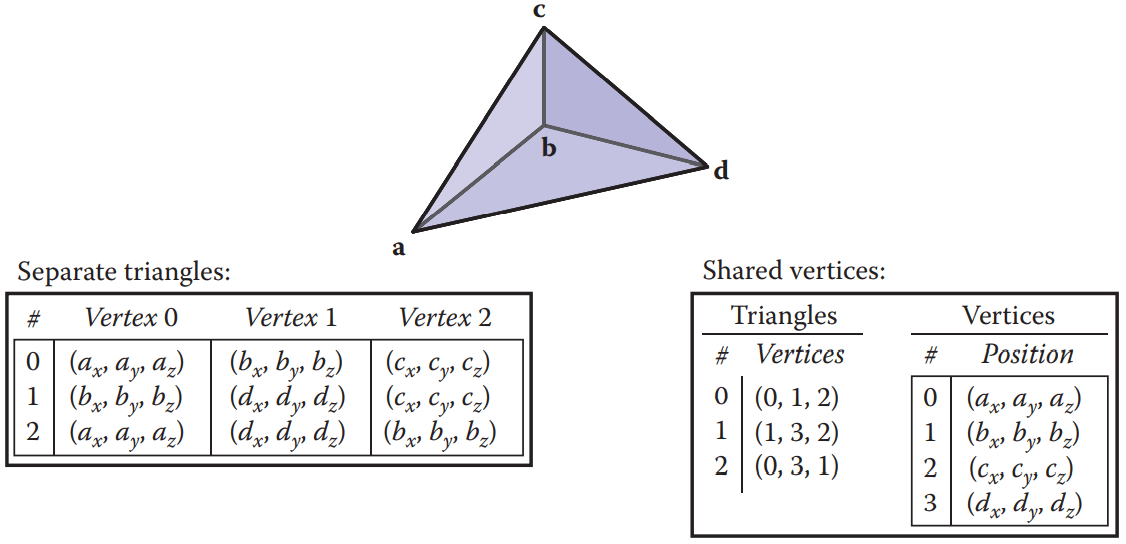
我们可以看到按三角形存储会造成额外的重复存储。

按三角形存储我们可以简单写成以下形式：

Triangle 
{
    Vertex v[3]
}

Vertex 
{
    vector3 position // or other vertex data
}

按顶点索引存储我们可一件简单写成：

IndexedMesh 
{
    int tInd[nt][3]
    vector3 verts[nv]
}

其中：

  • tInd：每个三角形顶点的索引
  • nt：三角形的索引
  • nv：顶点的索引

顶点索引存储是最常见的存储三角形网格，因为他很好地平衡了简单、方便、小巧。

我们想存储三角形的相邻三角形，顶点数据中包含该顶点的三角形。我们可以简单设置mesh的数据结构：

Mesh 
{
    // ... per-vertex data ...
    int tInd[nt][3]; // vertex indices
    int tNbr[nt][3]; // indices of neighbor triangles
    int vTri[nv]; // index of any adjacent triangle
}

我们可以接合下图来说明：

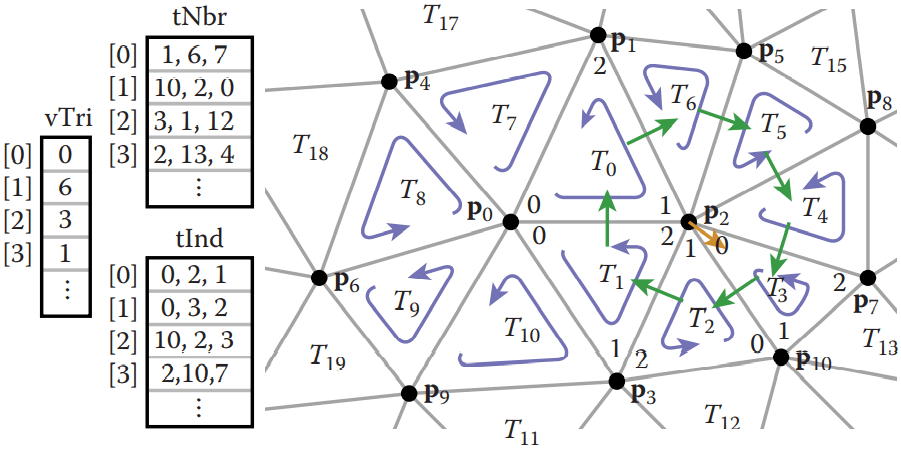
这其中和上面IndexedMesh的参数是一样，其他的为：

  • tNbr：三角形周围的三角形
  • vTri：顶点相邻的一个三角形(顺时针的下一个)

Winged-Edge

场景

我们在做物体顶点的转换时，需要注意矩阵相乘的顺序

function traverse(node)
    push(Mlocal)
    draw object using composite matrix from stack
    traverse(left child)
    traverse(right child)
    pop()

碰撞检测

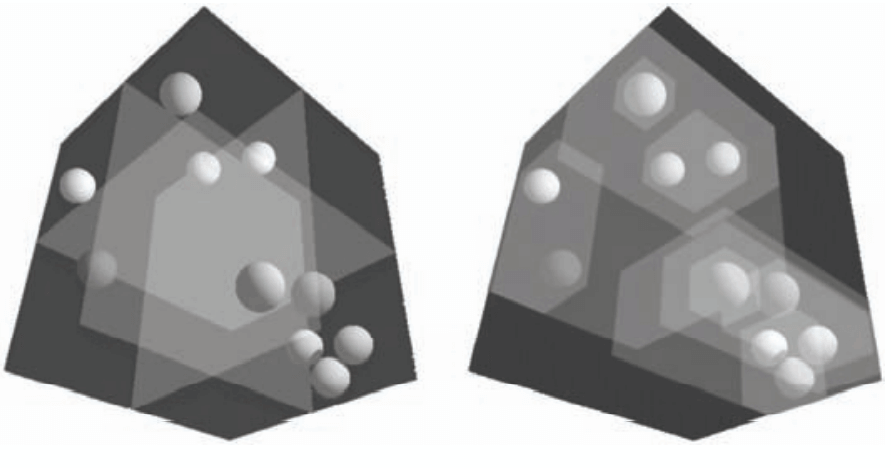
左图：空间的均匀划分。右图：包围盒划分

包围盒

我们从2d视角来看，也就是需要做的就是找到最左边、最右边、最下边、最上边的值。

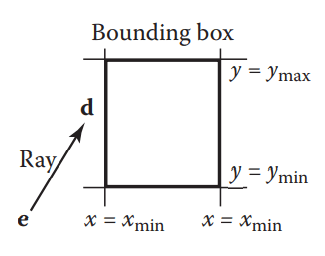
x=xmin,x=xmax,y=ymin,y=ymax.(x,y)∈[xmin,xmax]×[ymin,ymax].

分层包围盒

我们在检测碰撞时，可以设置包围盒。提前测试包围盒是否被射线穿过，然后再判断包围盒中的每个物体是否被穿透。这个看起来是减少了区域检测，但是我们在包围盒内部还是需要蛮力搜索。所以我们还可以把包围盒内部再次切割出不同的包围盒。

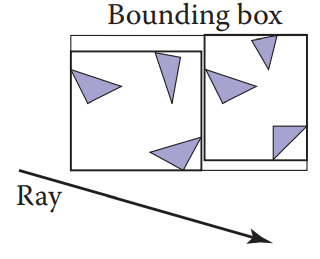
我们简单的伪代码可以写成这样：

if (ray hits root box) then
    if (ray hits left subtree box) then
        check three triangles for intersection
    if (ray intersects right subtree box) then
        check other three triangles for intersection
    if (an intersections returned from each subtree) then
        return the closest of the two hits
    else if (a intersection is returned from exactly one subtree)then
        return that intersection
    else
        return false
else
    return false

我们可以看到上面这种切分包围盒到更小的包围盒，然后始查询，这个查询其实是没有一定的顺序规则，先查询那个后查询那个。这里我们可以使用二叉树来管理，如下图：

把一个包围盒中的点分为灰色和黑色。我们可以简单的写出每个节点的数据结构：

class bvh-node subclass of surface
    virtual bool hit(ray e + td, real t0, real t1, hit-record rec)
    virtual box bounding-box()
    surface-pointer left
    surface-pointer right
    box bbox

实现一个碰撞的方法：

function bool bvh-node::hit(ray a + tb, real t0, real t1,hit-record rec)
    if (bbox.hitbox(a + tb, t0, t1)) then
        hit-record lrec, rrec
        left-hit = (left != NULL) and (left -> hit(a + tb, t0, t1, lrec))
        right-hit = (right != NULL) and (right -> hit(a+tb, t0, t1, rrec))
        if (left-hit and right-hit) then
            if (lrec.t < rrec.t) then
                rec = lrec
            else
                rec = rrec
                return true
        else if (left-hit) then
            rec = lrec
            return true
        else if (right-hit) then
            rec = rrec
            return true
        else
            return false
    else
        return false

这里就是递归检测分别检测左边右边时候有碰撞到。

我们可以使用一个轴来划分包围盒，这个轴可以是x=0,y=1,z=2这样的，同时我们可以划分两部分包含的物体的个数相等，这样的话我们可以减少二叉树中有很多单子叶的情况。

function bvh-node::create(object-array A, int AXIS)
    N = A.length
    if (N = 1) then
        left = A[0]
        right = NULL
        bbox = bounding-box(A[0])
    else if (N = 2) then
        left = A[0]
        right = A[1]
        bbox = combine(bounding-box(A[0]), bounding-box(A[1]))
    else
        find the midpoint m of the bounding box of A along AXIS
        partition A into lists with lengths k and (N − k) surrounding m
        left = new bvh-node(A[0..k], (AXIS +1) mod 3)
        right = new bvh-node(A[k + 1..N − 1], (AXIS +1) mod 3)
        bbox = combine(left → bbox, right → bbox)

统一空间细分

我们可以换一种思路，就是直接切分空间，我们把空间切分成很多个同一大小的区域。从二维的角度我们可以划分成下图：

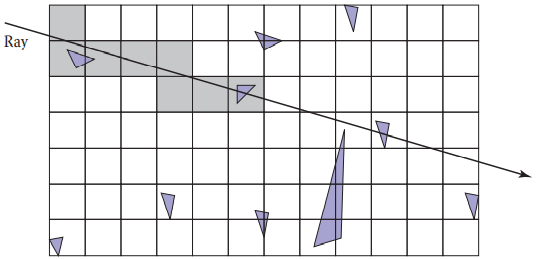
BSP

我们可以使用二分法的思路来对空间细分，这种做法叫做binary space partitioning。